九靈
纹明,《几何原本》来自中国的证据及其在西方的错误传播转载,作者:程碧波
学界认为,耶~稣~会数学家克拉维乌斯(Christoph Clavius, 1537/1538-1612)编注的《原本》1574年本前六卷被利玛窦(Matteo Ricci, 1552-1610)、徐光启(1562-1633)译成汉语并以《几何原本》书格链接 为题在1607年出版,是中国数学史上的重大事件,具有里程碑式的意义。不少权威数学史论著所列中国数学史分期方案都能支持这一点。
克拉维乌斯,著有《五卷本《克拉维乌斯“数学”著作全集》,其被其弟子利玛窦介绍到中国来的著作有《几何原本》《浑盖通宪图说》《乾坤体义》《同文算指》等书,据说其也是“格雷戈里历”应是格里高利历,见#18016、#18017的提出者。《几何原本》的著者欧几里得(Euclid),大约生活在公元前300年左右。当时希腊科学发展处于鼎盛时期,代表埃及、希腊数学成就最高水平的就是《几何原本》。这一数学史上最负盛名的巨著,不仅使许多数学著作相形见绌,而且对后世数学及自然科学的发展产生了极其深刻的影响,其数学思想和方法支配了数学两千多年。
网友文行先生根据徐光启翻译的《几何原本》中,徐光启的《序》里没有提及欧几里得,以及没有提及《几何原本》有后面九卷尚未翻译这两点,推断《几何原本》就是徐光启自己的作品,西方各版《几何原本》系对徐光启《几何原本》的抄袭。本文笔者仔细研读所谓徐光启翻译的《几何原本》,有极强的证据支持以下结论:
所谓徐光启所翻译的《几何原本》的核心内容才是中国本土原著的数学著作,而克拉维乌斯的《原本》(下称“克版”)以及其它西方版本的《原本》系抄袭自中国《几何原本》。其关键证据是:西方的《几何原本》所有版本均完全误读了中国的《几何原本》,因此产生了全面性的错误,而唯独徐光启版《几何原本》(下称“徐版”)是正确的。《(几何)原本》在西方的出现应不早于蒙古二次西征,即耶元1235年,其以西文形式的出现,应不早于耶元1400年,并且此《(几何)原本》应是残破的。❶ 徐光启版《几何原本》才是真正的原版《几何原本》。
一 “度”、“几何”与“量”的错误理解:西方《原本》体系的崩溃
(一)西方《原本》对“度”和“几何”的错误理解及其公理错误
克版为代表的所有西版《原本》从未真正理解“几何”之含义,这导致其大部分公理的错误和整本书的逻辑混乱。换言之,所有西版《原本》都是立不住的。而徐版正确阐述“度”、“几何”的含义,其公理正确,整本书结构和逻辑清晰。
徐版在卷一的“公论者不可疑”部分给出了几条公论(公理):
1、第一论:设有多度彼此俱与他等,则彼与此自相等。
2、第二论:有多度等,若所加之度等,则合并之度亦等。
3、第三论:有多度等,若所减之度等,则所存之度亦等。
4、第四论:有多度不等,若所加之度等,则合并之度不等。
5、第五论:有多度不等,若所减之度等,则所存之度不等。
6、第六论:有多度俱倍于此度,则彼多度俱等。
7、第七论:有多度俱半于此度,则彼多度亦等。
8、第八论:有二度自相合,则二度必等。
9、第九论:全大于其分。
克版在与以上九论对应的拉丁文中,没有字词与以上公论中的“度”相对应,而是使用了关系代词“那个(Quae)”。譬如第一论的拉丁文为“Quae eidem aequalia, et inter sesunt aequalia”。
在徐版卷一的“公论者不可疑”部分后续公论为:
1、第十四论:有几何度等,若所加之度各不等,则合并之差与所加之差等。
2、第十五论:有几何度不等,若所加之度等,则合并所赢之度与元所赢之度等。
3、第十六论:有几何度等,若所减之度不等,则余度所赢之度与减去所赢之度等。
4、第十七论:有几何度不等,若所减之度等,则余度所赢之度与元所赢之度等。
5、第十八论:全与诸分之并等。
徐版从第十四论到第十八论出现了“几何度”,那这“几何度”与第一论到第八论的“度”是一回事吗?如果是一回事,为什么后面突然出现“几何度”?徐版可能画蛇添足吗?
克版在与第十四论到第十八论对应的拉丁文中,同样没有与“几何度”对应的字词,对应的拉丁文为“aequalibus”与“inaequalibus”,意为等与不等。由此可知以上徐光启版《几何原本》中的“度”与“几何度”在克版的对应拉丁文中均无相关字词表达。
而目前流行的版本是标准的希思(Thomas Little Heath,1861-1940)英译评注本The thirteen bools of Euclid’s Elements(《欧几里得原本13卷》)。这个版本卷一中的公论大为减少,只有:1、等于同量的量彼此相等。2、等量加等量,其和仍相等。3、等量减等量,其差仍相等。4、彼此能重合的物体是全等的。5、整体大于部分。而其中“量”与“物体”的原文都是同一个词“thing”。很显然,其并没有第十四论到第十八论,也就不可能分辨“度”和“几何度”的区别。
由于西方所有版本《几何原本》的公论(公理)中均没有阐述“度”和“几何度”的区别,所以这所有版本中相对应的词均为“量(magnitudo)”或“连续量(quantitas continua)”。那现在来看看徐光启版《几何原本》如何解释“几何”,以及这种解释对于整本书的意义何在。
徐版卷五第一界:“分者,几何之几何也。小能度大,以小为大之分。以小几何度大几何谓之分。曰,几何之几,何者谓非?此小几何不能为此大几何之分也。如一点无分亦非几何,即不能为线之分也。一线无广狭之分,非广狭之几何,即不能为面之分也。一面无厚薄之分,非厚薄之几何,即不能为体之分也。曰,能度大者谓小几何,大几何能尽大之分者也。如甲为乙、为丙之分,则甲为乙三分之一,为丙六分之一,无赢不足也。若戊为丁之一即赢,为二即不足,己为丁之三即赢,为四即不足,是小不尽大,则丁不能为戊己之分也。以数明之:若四于八、于十二、于十六、于二十诸数皆能尽分,无赢不足也。若四于六、于七、于九、于十、于十八、于三十八诸数,或赢或不足,皆不能尽分者也。本书所论皆指能尽分者。故称为分。若不尽分者,当称几分。几何之几如四于六,为三分六之二(即三分之二),不得正名为分,不称小度大也,不为大几何内小几何也”。
这段话清晰地阐述了何为“几何”:某量可以被更小的某度来整除,此量即为大几何,此度即为小几何。若不能整除,就“不为大几何内小几何也”,换言之,就不叫几何。本段对不能整除的,给出了另一个专门名词“几分”。因此“几何”与“几分”是互补的概念。这段话还给出具体数字的例子:八除以四无余数,则四是八之小几何,八为四之大几何。六除以四有余数,所以四不是六的小几何,六不是四的大几何。故第二界就说:“若小几何能度大者,则大为小之几倍”。
徐版为何要如此定义“几何”呢?其卷五第四界说:“凡同理之比例有三种,有数之比例,有量法之比例,有乐律之比例。本篇所论皆量法之比例也”。因此,“几何”之定义,正是为“量法”,也即“测量之法”而产生的。因为在使用度量衡来测量物体时,度量衡一定有最小刻度,这个最小刻度的大小就是此度量衡能测量的最高精度。例若最小刻度是厘米,则其测量物体的最高精度就是厘米;若最小刻度是毫米,则其测量物体的最高精度就是毫米。按前段话,若最小刻度是四,则若将其来测量六,则要么为一度,要么为两度。实际上取一度时,少测量了二;取两度时,又多测量了二。只不过因为最小刻度为四,所以没有办法测量出二。要想测量出二,就必须采取最小刻度不大于二的更精密的度量衡。“几”的甲骨文是测量长度的刻度模样,“何”为“负荷”,即“测量值”。
图1 几,篆文
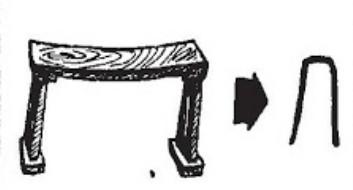
这就是现代分析数学中的测度论。
因此按现代的语言,“度”即是指“度量衡的刻度”,“几何”即是指“相对某特定刻度的可测量”。前述徐版第一论到第九论均是对“刻度”而言,第十四论到第十八论均是对“相对某特定刻度的可测量”而言,两者具有严格的区别。以第十八论“(几何度)全与诸分之并等”为例:以四为一度来测量六,假设采取四舍五入法,则测量得两度。如果有两个六分别测量再加总,则一共有四度。但是如果将两个六合在一起进行测量,则是以四来测量十二,测量得三度。显然分别测量之后加总测量值,与合并之后一次测量,其值不同。这就违反了“全与诸分之并等”的公论(公理)。同样地,《几何原本》中第十四到第十八公论均不再正确。只有可测量,也即“几何度”才满足第十四论到第十八论的公论。所以徐版中的“几何”二字绝不是可有可无的画蛇添足。
显然西方所有版本的《原本》都完全没有弄明白《原本》的真正意思。因此西方版的《几何原本》把“度”和“几何度”均混同为形体的客观真实数值而未认识到是刻度和测量值。自然地,西方所有版本的《原本》对这些公论的证明都是错误的。
(二)“几何”是中国自古就有数学测量体系
通常认为“几何”是徐光启借用中国传统上“几何”的“多少”、“数量”之意,同时谐音西方“Geometry”或“Magnitude”而得。但是中国自古对于“几何”就有极为准确的定义。
第一,“几”的含义虽然是“多少”或“数量”,但它却是指“整数的多少”或“整数的数量”。而这正是徐版《几何原本》中“几”的关键性含义。西方各版《原本》均没有理解此含义,导致其整个公理体系的错误,和全书体系的混乱。
第二,中国古代正是用“几”来进行度量,“几”是度量衡。《周礼.考工记》说:
“室中度以几,堂上度以筵,宫中度以寻,野度以步,涂度以轨”
其意思是说:“室中用几来度量,堂上用筵来度量,宫中用寻来度量,野地用步来度量,道路用车轨来度量”。所以“几何”正是“以度量衡来测度所得数值”的意思。这个数值必然是度量衡最小刻度的整数倍。这与西方各版《原本》中与度量衡完全无关的“量”的概念截然不同。
第三,由于“几”的数值为整数,则当被测量物体的数值不满足最小刻度的整数倍时,需要作近似处理为整数倍。所以中国的“几”又表示“近似(取整)”之意。如:贾谊《论积贮疏》:“汉之为汉,几四十年矣”。此即“几乎”之来历。
所以“几何”一词,正是中国自古以来的测度术,它的内容正是徐版《几何原本》的内容。
从数学难度看,《几何原本》的内容主要是“度”和“几何度”的计算以及量纲换算,只有简单的比例方法和部分无理数判别方法,其连分数计算方法和无理数计算方法都没有。因此其数学难度远不及《九章算术》《缀术》《九章算术注》《数书九章》等内容,中国自古以来的测度术完全有能力包含《几何原本》的内容。事实上并非“几何”二字来自“Geometry”的音译,相反乃是“Geometry”来自“几何”的音译。可惜的是“Geometry”翻译到了“几何”的音,却完全不理解“几何”之含义。
(三)西方《原本》因错误理解“度”和“几何”而致的体系崩溃
徐版区分了有理数和无理数的测度。其卷五第三界说:
“凡比例有二种,有大合有小合,以数可明者为大合,如二十尺之线比十尺之线是也。其非数可明者为小合,如直角方形之两边与其对角线可以相比而即非数可明者是也......即分至万分以及无数,终无小线可以尽分能度两率者是也。”
因此徐版已经阐述了今天的有理数和无理数,并且将有理数比例称为大合,无理数比例称为小合。并指出小合之时,无论刻度的精度多高,都不可能量尽小合比例。换言之,对于无理数之测量,就会出前述“分别测量之后加总测量值,与合并之后一次测量,其值不同”的同类问题,因此前述公论第十四到第十八均不再正确,产生了由于精度有限而导致的误差,因此为小合。绝非克版在内的所有西方《原本》那样均以为前述公论在任何情况下均适用。克版在内的所有西方《原本》那样均以为前述公论在任何情况下均适用的原因在于:它们误以为这些公论的对象是形体的客观真实值。
在徐版中,“大合”乃指“完全精确之合”,“小合”,乃指“由于精度有限而导致的有误差之合”。那么,对于小合如何处理呢?徐版《几何原本》卷一第四十七题明确指出:“以开方尽实者为例,其不尽实者自具算家分法”。因此徐版指出,对无理数的处理,要通过算术系统来完成(中国算术系统在《墨经》中已经称呼无理数为“面”,在《周髀算经》时代已经可以通过割圆术计算无理数)。其实其讲“即分至万分以及无数,终无小线可以尽分能度两率者是也”,这已经在讲算术系统。
这就解释了为什么《几何原本》仅仅给出了无理数的比例规则,并未给出无理数的计算规则,因为徐版认为对无理数的计算属于算术系统,也即代数系统的范畴。虽然徐光启在序中对《几何原本》推崇备至,但是徐版正文中非常清晰地给出了本书的定位。徐版还直接引用了分数计算的“通分”而未详述之,这也说明本书认为通分不属于《几何原本》的内容,《几何原本》拿来用即可。这也解释了《几何原本》中为何没有分数计算系统。
徐版同时清晰地区分了“度”和“几何”的可分性和不可分性。
其卷一第四求中说:
“设一度于此,求作彼度较此度或大或小。或言较小作大可作,较大作较小不可作。何者,小之至极,数穷尽故也。此说非是。凡度与数不同。数者可以长不可以短,长数无穷,短数有限。如百数减半成五十,减之又减,至一而止。一以下不可损矣。自百以上增之可至无穷。故曰,可长不可短也。度者可以长,亦可以短。长者增之可至无穷,短者减之亦复无尽。当见庄子称一尺之棰,日取其半,万世不竭,亦此理也。何者,自有而分,不免为有。若减之可尽,是有化为无也。有化为无,犹可言也,令已分者更复合之,合之又合,仍为尺棰。是始合之初,两无能并为一有也。两无能并为一有,不可言也。”
本段话的含义是:刻度是可以任意大,也可以不断细分至任意小的;而几何,也即几何数值,可以无穷大,但其最小值为一,不能任意小。这个解释非常清楚:刻度可以根据需要而任意调节大小,但是以既定刻度测量出的几何数,一定是刻度的整数倍数,不可能出现分数,因为刻度本身就是最高的精度,无法表达出比刻度更小的分数精度。所以刻度可任意小而几何数不可任意小。
由于西方版本《几何原本》把“度”与“几何”混同为“形体的真实值”,所以德谟克利特和他的老师留基伯把中国“几何”的不可细分性,误认为线段、面积和立体这些数学形体的真实值是由有限个不可再分的原子构成。亦由此可知,所谓德谟克利特出生于公元前五世纪的观点也是不正确的。同时这也导致了西方否定零和负数。但徐版其实是说“测量所得的几何数”不能为零或负数,因为如果为零,形体不存在,就不必测量。形体的值也不可能为负。这完全是从测量的前提来说的,但不是说在其它情况下也没有零或负数。
综合来看,长期困扰西方的几乎所有数学问题,都是因为看了但不理解中国《几何原本》中“测量”的前提而产生的。西方所谓从古至今的几乎所有数学争议、哲学争议乃至物理学争议的渊源均来自对徐版《几何原本》的错误解读。由于中国《几何原本》中缺了分数计算系统和小数计算系统,缺了位值进制的级数系统,整个西方数学亦跟着缺了相应部分。
因此,西方科学的全部体系,的确是建立在中国《几何原本》基础上的。
当“度”可以任意小后,“此刻度”与“彼刻度”下所测得的几何值必然就不同,需要进行彼此的单位换算,也即量纲换算,以分析数学的语言来说,就是“测度变换”。在进行测度变换时,由于“此刻度”与“彼刻度”之间再无整数的比例关系限定,所以两种刻度之比既可能是整数,亦可能是分数,亦可能是无理数。《几何原本》中的比例计算部分,事实上就是在阐述测度变换,通俗来说就是单位换算,也即量纲换算。
因此徐版的结构是清晰的:从点线面体定义开始,阐述测量的刻度(大家熟悉的全等研判等内容,事实上就是在研究刻度,因为刻度与刻度之间必须相等)、根据刻度进行测量的几何,再阐述测度变换的比例计算,再阐述测度变换中出现的分数和无理数比例,并将具体数值的计算归于算术系统,也即代数系统。其设计的数学题也朴实而紧扣主题。这吻合徐版说“凡同理之比例有三种,有数之比例,有量法之比例,有乐律之比例。本篇所论皆量法之比例也”。
故《几何原本》用今天的话来说,是《测量与单位换算之书》,精炼地说即《可测量之原理》,更简地说即《测度原理》。
其测量精度的阐述,清晰解释了几何度的公理不适于非几何度,绝非西方《原本》那样弄个“连续量”就认为公理可以普适了。徐版能清晰地解释现代测度学中关于有限或无限的诸多悖论。反观包括克版在内的西方《原本》,把“度”、“几何”和“真实数值”混为一谈,其体系结构杂乱无章,乱套公理,也无法解释为什么缺乏分数系统和算术系统。
克版序言中说:
“因此欧几里得,几何学的大师,打算在《原本》中以不带任何数字的方式传授几何学的完美知识,他在前六卷中处理平面几何,在后五卷中处理立体几何,极为清楚地探讨了这些图形的性质”。
显然欧几里得没有想到真正的《几何原本》恰恰是为数字服务,其核心正是研究欧几里得最看不起的测量精度和测量单位换算问题。❷
二 非欧几何与几何之阶数
徐版阐述了今所谓非欧几何,这就是曲线角和杂线角。在其卷一第八界中说:
“平角者,两直线于平面纵横相遇交接处”。
第九界:
“直线相遇作角为直线角。平地两直线相遇为直线角,本书中所论止是直线角。但作角有三等,今附著于此,一直线角,二曲线角,三杂线角,如下六图”:
图2 徐光启版《几何原本》:直线角、曲线角和杂角
“平角”是指“角”的形状为平直,且因纵横相遇而无零度和一百八十度角。直线角则有零度和一百八十度角。曲线角和杂线角之两边则可能为曲线,且不一定在同一平面。
而克版对应的部分不是“平角”,而是“平面角,即两线在平面上倾斜接触,但并不彼此融合为一条线”。“平面角”只是说“角”的边线在同一个平面上,但“角”的边线不一定是直线,但因“倾斜”所以无零度或一百八十度角,所以克版的定义是有缺陷的。此外,不在同一平面上的曲线角和杂角没有纳入克版中。所以徐版所说的“但作角有三等”的确是囊括了平面和立体情况下所有的角的可能。克版是不能称之为“但作角有三等”的。而非欧几何正是研究曲面上的图形关系。所以徐版的曲线角、杂线角正是非欧几何之渊源,而克版的曲线角、杂线角则不是。徐版说:“本书中所论止是直线角。但作角有三等,今附著于此,一直线角,二曲线角,三杂线角”,说明在《几何原本》之外尚有专门论述非平面的曲线角和杂线角的著作,这就是后来的非欧几何。
现在通行的希思版则连“曲线角”和“杂线角”的阐述都没有,而是突兀地抄了徐版卷三第十六题:“圆径末之直角线全在圆外,而直线偕圆界所作切边角,不得更作一直线入其内。其半圆分角大于各直线锐角。切边角小于各直线锐角”,突然冒出来一个“切边角”和“半圆(分)角”。所谓“切边角”如下图3:
图3 徐光启版《几何原本》:切边角
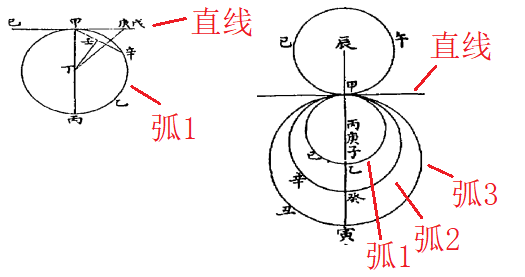
图3是徐版《几何原本》中的切边角,是圆弧与切线所构成的角,角的一边是切线,另一边是弧线。图3左边标注“直线”和“弧1”为边的角为切边角,图3右边标注“弧1”与“直线”、“弧2”与“直线”、“弧3”与“直线”构成三个切边角。图中还有其它切边角,因未标出所以不赘述。图3左边是“甲辛”线无法两分“弧1”和“甲戊”直线构成的切边角。图3右边,“弧1”与“直线”构成的切边角可以被“弧2”与“直线”构成的切边角、以及“弧3”与“直线”构成的切边角所分。
切边角无法被直线两分的原因是圆的切线与圆弧的夹角在切点处趋于零。所以任意不为零的直线角都大于切边角。但徐版并未停留在此,而是进一步深入阐述一个重要命题,也即卷十第一题:
“设一小几何,又设一大几何,若从大者半减之,减之又减,必至一处小于所设小率。”
但图3中直线角无论如何递减半,其都大于切边角,故卷十第一题似乎不对。但徐版认为切边角趋于无穷小,而直线角有限小,所以切边角不是直线角的小几何,故不满足卷十第一题“大几何”与“小几何”的条件。如果大几何与小几何均为切边角,就可以用小切边角来分大切边角,卷十第一题的结论就正确了。徐版很清楚这是由于度与被度的数具有不同阶数所致:大几何与小几何必须同阶。因此徐版说:
“彼所言大小两几何者,谓夫能相较为大,能相较为小者也。如以直线分直线角,以圆线分圆线角。是已,此切边角与直线角岂能相较为大小哉?”
所谓“相较为大、相较为小”,不是“比较大、比较小”,乃是指“小几何不断以半率增加成为大几何、大几何不断以半率减少成为小几何”。所以徐版说:
“有两种几何,一大一小,以小率半增之,递增至于无穷。以大率半减之,递减至于无穷,其元大者恒大,元小者恒小。”
这句话的含义是:若大几何不断减半,小几何不断增半。无论递增和递减到什么时候,大几何都大于小几何,则大几何与小几何不能相较为彼此。这是徐版对“阶数”的正确描述。
而克版的表述是:
“第十卷第一条命题是这样的:如果从两个不等连续量(quantitas)中较大的一方减去一个大于它的一半的连续量,然后继续从余下的连续量中减去它的一半,减而又减,剩余的连续量就会小于所设较小的连续量……同类角的相等需要两线之间相同的倾斜程度……而在切边角和半圆角中无法找到相等的倾斜程度,因为(当两角重叠时)它们的线并不重合,而是互相乖违......第十卷第一条命题只能适用于任一个均能增长到超过另一个的几何,无论它们是同类几何还是异类几何。而这并非切边角和直线锐角的情况”。
克版与徐版的表述有两大不同。首先,克版使用的是“连续量”而不是“大小几何”。显然直线角和切边角都是连续量,但是直线角连续量再怎么递减半,亦不可能小于切边角连续量。所以按照克版的表述,第十卷第一条命题就是错的。其次,克版是从切边角与直线角永远没有相等的倾斜程度的图形辨识角度,来判定切边角怎么增长也无法超过直线角。而徐版是阐述了另一个规则:“一个大量递减半,一个小量递增半,如果小量始终小于大量,则此两量不能相较为彼此,也即不能为大几何与小几何”。
这已经不限于直线角和切边角,而是普适性的高阶无穷小量判别。这才是真正的数学分析。希思版的《几何原本》第十卷命题一说:“给出两个不相等的量,若从较大的量中减去一个大于它的一半的量,再从所得的余量中减去大于这个余量一半的量,并且连续这样进行下去,则必得一个余量小于较小的量”。其没有提及大量和小量的阶数问题,也没有提及小量是大量的小几何的问题,其错误就更大了。
作为刻度确定、测量及单位换算的《几何原本》,既不是数学逻辑的起点也不是数学逻辑的终点。西方版《几何原本》卷一从定义“点”、“线”、“面”开始定义,这似乎是逻辑的起点,但其实并不对。希思版说:“直线是它上面的点一样地平放着的线”、“平面是它上面的线一样地平放着的面”、“等量加等量,其和仍相等”。那么何谓“平放”?显然是讲不清楚的。又如“相等”,应该是“一定前提下A和B可以相互置换而不影响结果,此谓A与B相等”,因此定义中要有前提、有结果,然后可说“相等”,否则“相等”亦模糊不清。这是西方版《原本》被诟病的真正根子。因此《几何原本》中的定义不可能是逻辑起点,相反,它必须要引入物理的实体世界来补充逻辑起点。徐版很清楚这点,因此在正文中写“直线之中点能遮两界”、“平面中间线能遮两界”、“用一直绳拖于角,绕面运转,不碍于空,是平面也”。前两者均用物理世界的光线来定义直线和平面,最后者用力学来定义直线和平面。在这样的定义下,《几何原本》的基础才牢不可破。西方一直到后来的牛顿,其在《自然哲学之数学原理》里面才意识到力学是《原本》的逻辑基础。西方版《原本》由于没有物理判据乃至鄙视物理判据,错误地把《原本》理解为纯粹形而上学的数学理论书籍,因此其“直线”、“平面”和“等于”等概念不可能讲清楚,必然出现混乱。但这种混乱并非非欧几何产生的根源,徐版中的曲线角、杂线角才是非欧几何产生的根源。
要建立纯粹的形式逻辑的数学系统当然亦可以,但此数学系统的逻辑起点恰恰必须是在代数符号系统。需要首先构造“数字符号系统”,再用数字符号系统来构造“加减乘除”、“等于”等原子操作。完成这些逻辑准备后,才可以进一步按勾股关系来定义“距离”、按等比关系来定义“直线”。数学系统的逻辑终点在于完成刻度选择及其单位换算后计算出测量结果。起点和终点都是算术系统。《几何原本》恰恰是最具应用性的测量工具的算法,它来自中国工匠们拿着具有刻度的尺规来进行测量,以及在不同单位制下对测量值进行单位换算的社会实践,绝非坐在书斋中的所谓古希腊学者们鄙视刻度数字而臆造出的完美的形而上学的东西。
克版中亦讲了光学研判标准,但却搁在注释部分,因此其对于物理判据的重要性是缺乏认识的。在他看来,这只是补充的形象化说明,而不是《几何原本》逻辑体系的基础。克拉维乌斯、欧几里得等人都厌恶物理世界的引入,而误以为这是一本完全形而上学的书❸。
综上所述,本文研判,包括克拉维乌斯拉丁文《原本》在内的所有西方《(几何)原本》,抄袭了中国《几何原本》,抄袭了中国《几何原本》关于“度”和“几何”的公理等命题,汲取了中国《几何原本》关于“几何”不可无限分、“几何”为整数、不可为零、不可为负等阐述,但又不理解中国《几何原本》中“度”和“几何”在测量上的真正含义,而用“量”或“连续量”将两者混淆,并将其误以为是形体的客观真实数值,出现了主要公理等命题的错误及证明的体系错误。西方所谓自古以来的数学争论、哲学争论乃至物理争论,均是没有理解中国《几何原本》中“测量”的前提所致。这也导致了西方版《(几何)原本》在结构上的混乱和不成体系。但是,不能研判西方所有《(几何)原本》均是徐光启版本所标注年代之后才产生,蒙古二次东征可能已经携带部分《原本》到欧洲。但根据本系列文章的证据,《(几何)原本》在西方的出现应不早于蒙古二次西征,即耶元1235年,其以西文形式的出现,应不早于耶元1400年,并且此《(几何)原本》应是残破的。徐光启版《几何原本》才是真正的原版《几何原本》,利玛窦将其送回欧洲,以克拉维乌斯的名义发表,所以克拉维乌斯版《原本》尤其在注释部分出现了算术特色的很多内容。但是克拉维乌斯版仍然没有理解中国版《几何原本》的精髓。就徐光启本人,亦很难说真正读懂了中文《几何原本》,否则他应能指出西文《原本》的基础性错误。中国本土的《几何原本》即使对于今天的数学思想前沿、哲学思想前沿、物理学思想前沿,也将起着拨云见日的重要作用。


