九靈
平方法例题:
《兼济堂汇编刻梅勿庵先生历算全书》(雍正癸卯元年1723年刻印发行,美国国会图书馆藏),筹算 卷二:平方法。
题:假如有积一千,平方开之。
算法:
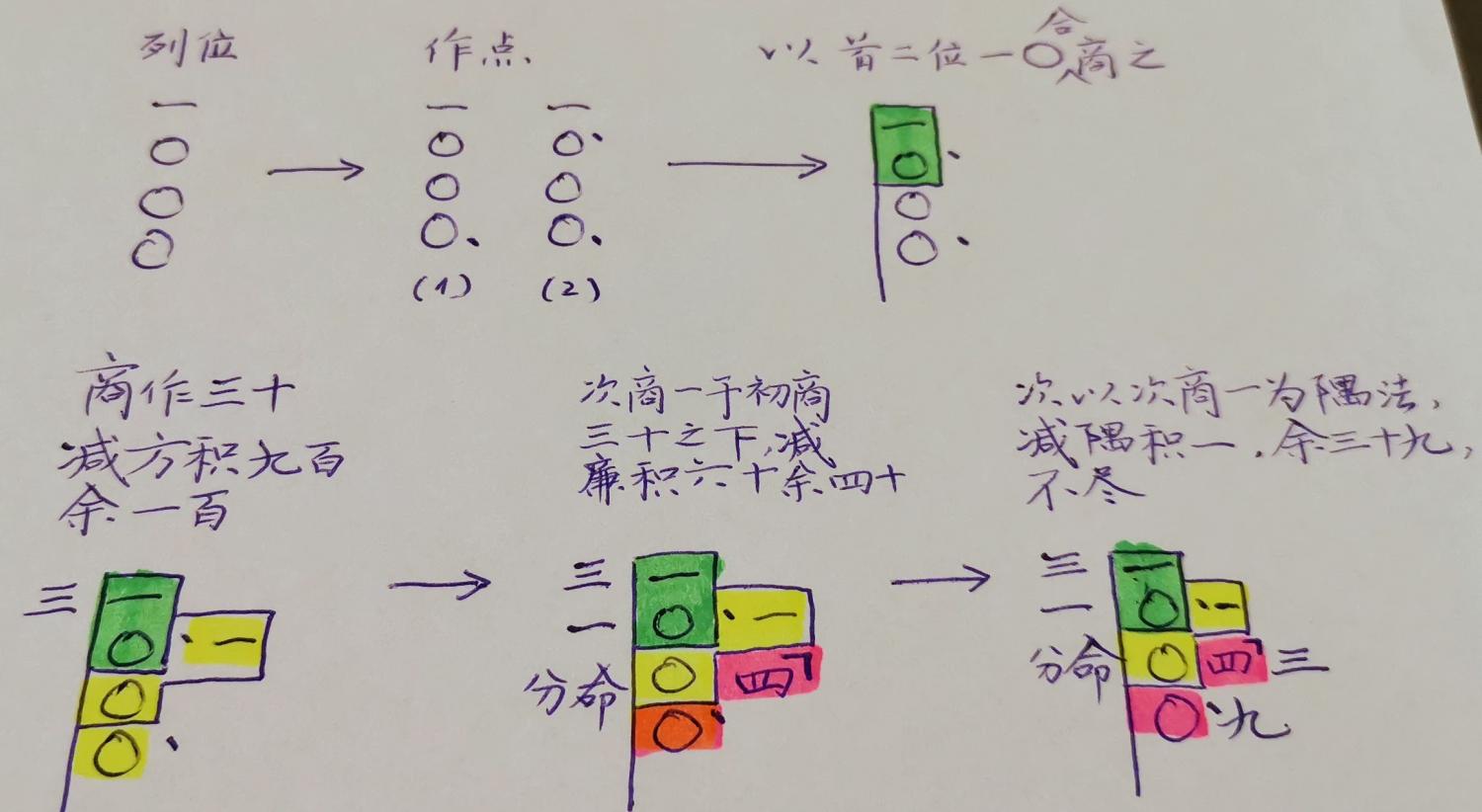
(一)、“列位”
(二)、“作点”。作点的方法,从单位(个位)开始,从低位到高位,隔位以点作标记。
(三)、“视点在次位,以首二位一千〇百①合商之。”这句话是说,看两个点,高位的那个点不在首位,在第二位,因此用首次两位取初商。
(四)、“乃视平方筹小于一〇者,〇九也,〇九之方三。商作三十。”这句话是说,看平方筹,在筹上找比10小的最大的积,此处为9, 而9的平方根是3,因此,初商的值是30。因为有两个点,所以初商是两位数。
(五)、“减方积九百,余一百。”
(六)、“次以初商三十,倍作六十②,用第六筹为廉法。”
(七)、“视第六筹第一行③是〇六,小于一百,次商一于初商三十之下。”再看第六筹,第二行是12,这里表示120,比100大,不合适,再看第一行是6,这里表示60, 比100小,所以记1(第一行)到3下面。
(八)、“次以次商一为隅法,减余积一④,余三十九不尽。”
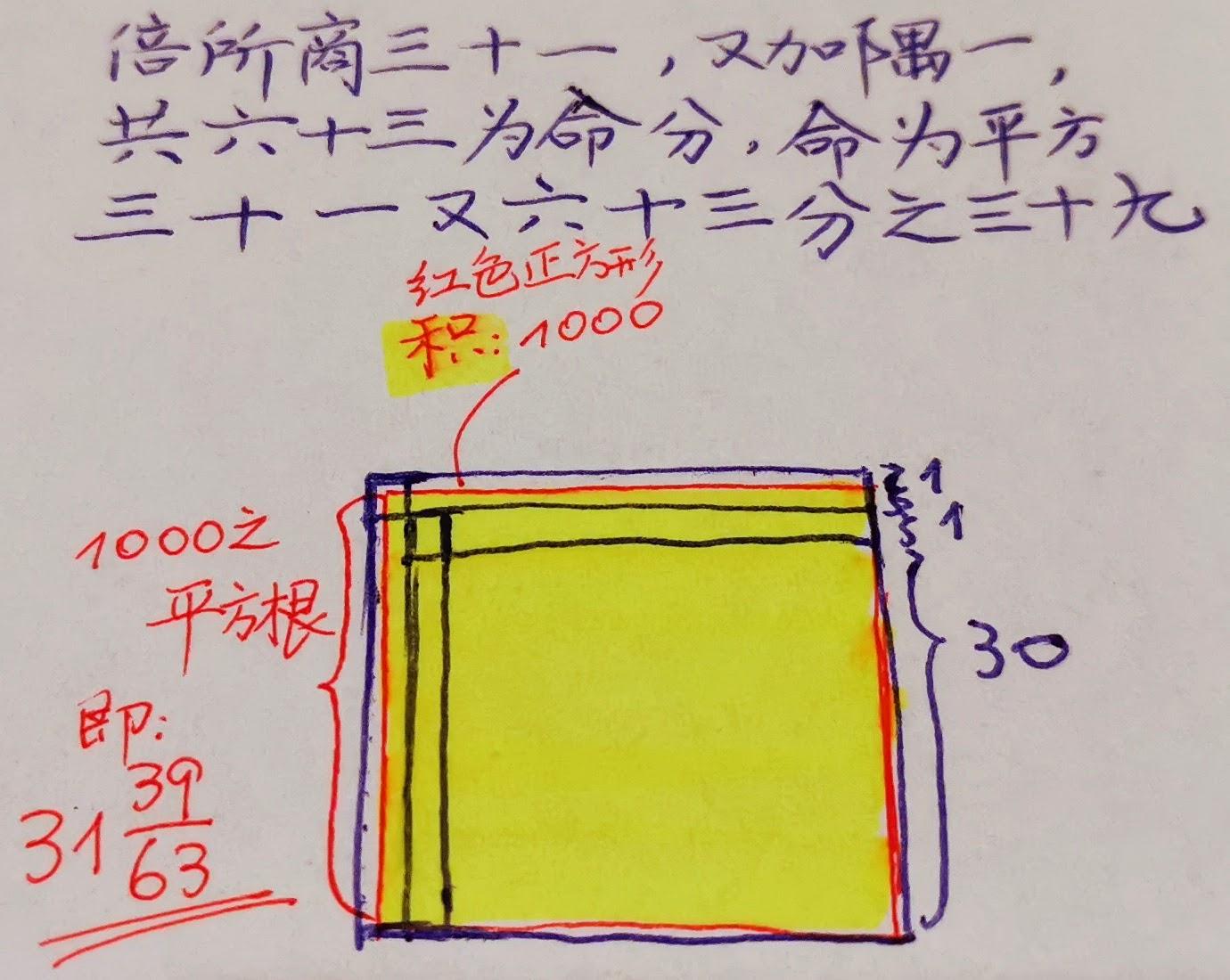
(九)、“所开以至单位,而有不尽,以法命之⑤。倍所商三十一,又加隅一,共六十三为命分,命为平方三十一又六十三分之三十九。”至此已经开到个位,还有余数,因此,要用命分法(分数)来计算余下的部分。命分法的本质是 再作两个宽为1(最小的整数)的次廉(矩形)和一个边长为1的隅(小正方形),这样就得到 了一个边长32的正方形,积为1024,1024大于题目所给的1000,所以只取其中的一部分,即39/63。这样,得到的积正好1000。
注:
①,空位,表示无,即零。此处“一千〇百”即表示千位记一,而百位记零,即1000。
②,初商外有次商,以初商乘次商(长x宽)得廉积(矩形面积),廉积有两个,因此初商需乘以二。
③,古书从上往下,从右往左书写或者阅读,所以“行”指从上往下垂直的一行(现在叫列)。
④,如此,方积+两廉积+一隅积正好又是一个正方形。但是和题目给的积(正方形)一千还差三十九。看图,初商+次商=31,即一方两廉一隅形成的大一点的正方形边长31,如果我继续以31寻找两个矩形(廉积)的话,就找不到了,因为即使取最小的整数为1,两个矩形面积之和为62,大于39。所以叫作“余三十九不尽”。
⑤,“命分法曰,但开至单数而有余实者,是不尽也。不尽者,以法命之。法以所开得数倍之,又加隅一为命分,不尽之数为得分。凡得分,必小于命分。”
图 计算过程